Main menu
You are here
What is Golden Ratio
What is Golden Ratio
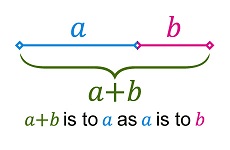
When you draw some rectangles , you will like some of them more than the others ,, and if you want to know why , you should know what it's called ( THE GOLDEN RATIO ). The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric figures such as the pentagon, pentagram, decagon and dodecahedron.
It is denoted ![]() , or sometimes
, or sometimes ![]() .
.
There are alot of examples of the golden ratio :-
The Great Pyramid of Giza built around 2560 BC is one of the earliest examples of the use of the golden ratio. The length of each side of the base is 756 feet, and the height is 481 feet. So, we can find that the ratio of the vase to height is 756/481=1.5717.. The Rhind Papyrus of about 1650 BC includes the solution to some problems about pyramids, but it does not mention anything about the golden ratio Phi.
Definitions of Golden Ratio
1) Numeric definition
Here is a 'Fibonacci series'.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ..
If we take the ratio of two successive numbers in this series and divide each by the number before it, we will find the following series of numbers.
1/1 = 1
2/1 = 2
3/2 = 1.5
5/3 = 1.6666...
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538...
34/21 = 1.61904...
The ratio seems to be settling down to a particular value, which we call the golden ratio(Phi=1.618..).
2) Geometric definition
We can notice if we have a 1 by 1 square and add a square with side lengths equal to the length longer rectangle side, then what remains is another golden rectangle. This could go on forever. We can get bigger and bigger golden rectangles, adding off these big squares.
Step 1 Start with a square 1 by 1
Step 2 Find the longer side
Step 3 Add another square of that side to whole thing
Here is the list we can get adding the square;
1 x 1, 2 x 1, 3 x 2, 5 x 3, 8 x 5, 13 x 8, 21 x 13, 34 x 21.
with each addition coming ever closer to multiplying by Phi.
start 1 by 1, add 1 by 1 => Now, it is 2 by 1, add 2 by 2
![]()
![]()
Now, it is 3 by 2, add 3 by 3 => Now, it is 5 by 3, add 5 by 5

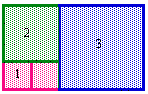
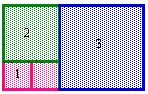
Now, it is 8 by 5.
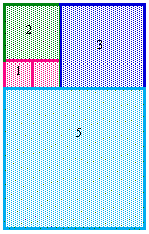
3) Algebraic and Geometric definition
We can realize that Phi + 1 = Phi * Phi.
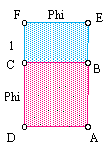
Start with a golden rectangle with a short side one unit long.
Since the long side of a golden rectangle equals the short side multiplied by Phi, the long side of the new rectangle is 1*Phi = Phi.
If we swing the long side to make a new golden rectangle, the short side of the new rectangle is Phi and the long side is Phi * Phi.
We also know from simple geometry that the new long side equals the sum of the two sides of the original rectangle, or Phi + 1. (figure in page4)
Since these two expressions describe the same thing, they are equivalent, and so
Phi + 1 = Phi * Phi.
II. Some Golden Geometry
1) The Golden Rectangle
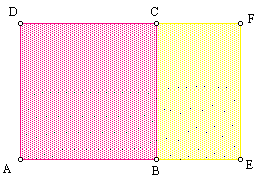
A Golden Rectangle is a rectangle with proportions that are two consecutive numbers from the Fibonacci sequence.
The Golden Rectangle has been said to be one of the most visually satisfying of all
geometric forms. We can find many examples in art masterpieces such as in edifices of ancient Greece.
2) The Golden Triangle
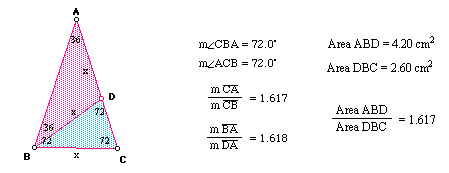
If we rotate the shorter side through the base angle until it touches one of the legs, and then, from the endpoint, we draw a segment down to the opposite base vertex, the original isosceles triangle is split into two golden triangles. Aslo, we can find that the ratio of the area of the taller triangle to that of the smaller triangle is also 1.618. (=Phi)
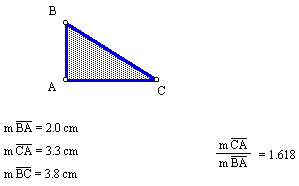
If the golden rectangle is split into two triangles, they are called golden triangles suing the Pythagorean theorem, we can find the hypotenuse of the triangle.
3) The Golden Spiral
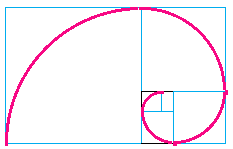
The Golden Spiral above is created by making adjacent squares of Fibonacci dimensions and is based on the pattern of squares that can be constructed with the golden rectangle.
If you take one point, and then a second point one-quarter of a turn away from it, the second point is Phi times farther from the center than the first point. The spiral increases by a factor of Phi.
This shape is found in many shells, particularly the nautilus.

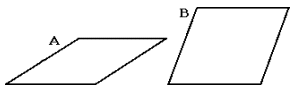
4) Penrose Tilings
The British physicist and mathematician, Roger Penrose, has developed an aperiodic tiling which incorporates the golden section. The tiling is comprised of two rhombi, one with angles of 36 and 144 degrees (figure A, which is two Golden Triangles, base to base) and one with angles of 72 and 108 degrees (figure B).
When a plane is tiled according to Penrose's directions, the ratio of tile A to tile B is the Golden Ratio.
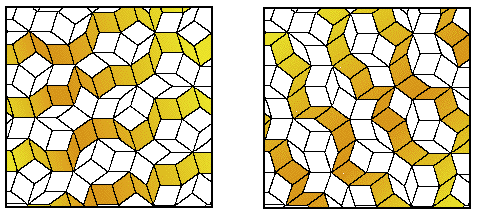
In addition to the unusual symmetry, Penrose tilings reveal a pattern of overlapping decagons. Each tile within the pattern is contained within one of two types of decagons, and the ratio of the decagon populations is, of course, the ratio of the Golden Mean.
5) Pentagon and Pentagram
We can see there are lots of lines divided in the golden ratio. Such lines appear in the pentagon and the relationship between its sides and the diagonals.
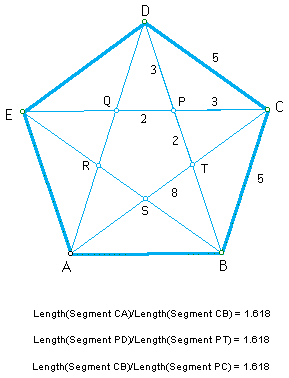
We can get an approximate pentagon and pentagram using the Fibonacci numbers as lengths of lines. In above figure, there are the Fibonacci numbers; 2, 3, 5, 8. The ratio of these three pairs of consecutive Fibonacci numbers is roughly equal to the golden ratio.
III. Golden Ratio in Art and Architecture
A. Golden Ratio in Art
1) An Old man by Leonardo Da Vinci
Leonardo Da Vinci explored the human body involving in the ratios of the lengths of various body parts. He called this ratio the "divine proportion" and featured it in many of his paintings.

Leonardo da Vinci's drawing of an old man can be overlaid with a square subdivided into rectangles, some of which approximate Golden Rectangles.
2) The Vetruvian Man"(The Man in Action)" by Leonardo Da Vinci
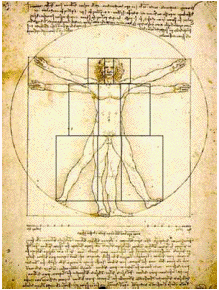
We can draw many lines of the rectangles into this figure.
Then, there are three distinct sets of Golden Rectangles: Each one set for the head area, the torso, and the legs.
3) Mona-Risa by Leonardo Da Vinci

This picture includes lots of Golden Rectangles. In above figure, we can draw a rectangle whose base extends from the woman's right wrist to her left elbow and extend the rectangle vertically until it reaches the very top of her head. Then we will have a golden rectangle.
Also, if we draw squares inside this Golden Rectangle, we will discover that the edges of these new squares come to all the important focal points of the woman: her chin, her eye, her nose, and the upturned corner of her mysterious mouth.
It is believed that Leonardo, as a mathematician tried to incorporate of mathematics into art. This painting seems to be made purposefully line up with golden rectangle.
As you can see , its really complicated, but it really worths reading about it.
"what is golden ratio"

